The way calcSD gets its results is simple. There are many studies out there that try to determine the average penis size and the distributions of length and girth. All this website does is take data from these studies and process it. In this page you can read more about the studies and the calculations done.
The Datasets
The calculations use data from the dataset you select, each dataset has an average (a.k.a. mean) and a standard deviation for each dimension (length, girth, flaccid, etc.). More info about each one is available on the Dataset List page. There's also a small table under the main calculator for a quick reference on each dataset.
The calculator's default dataset is the recommended global average, but you can choose other ones as well. Feel free to compare them. Outdated ones are marked as such and using those is generally not recommended. The individual studies themselves are usually only based on a small sample of the population, but they are reliable enough for general purposes. As always, don't get too attached to the statistics.
If you feel like the studies are wrong or if you are skeptical about it, this page might help you.
The Calculations
The hosting service used does not allow for any server-side processing, which means that everything has to be done via JavaScript (ex. if there's a need to do an addition to get a value, your browser does the addition while the page is open rather than the server doing the addition and transmitting the result to you), which restricts what can be done with the website.
Using an average and a standard deviation, the website calculates a z-score (a.k.a. standard score), which represents how many standard deviations you are above or below average. For example, if the average length is 13cm and the standard deviation is 1cm, then at 14cm your z-score would be +1 which is one SD above the mean. At 16cm you'd have a z-score of +3, at 11cm you'd have a z-score of -2 and so forth.
Afterwards, it will convert the z-score into a percentile. It assumes a normal distribution, which is consistent with analysis of normalcy of reported results in studies (the log-normal, while a more mathematically correct model, tends to add very excessive right skew inconsistent with the data at both left and right tails). This is only an approximation, but if penis size is not under appreciable selection, then it is likely to be an accurate approximation.
After a percentile is calculated, it's not difficult to use that rarity to compare against a room of n guys in the end. Fun fact: the 0 and 100 percentiles don't exist. Saying you're in the 99 percentile means you're higher than 99% of the population, but saying you're on the 100 percentile means you're higher than 100% of the population, including yourself... which is a contradiction. Same goes for the 0 percentile but in reverse.
We also use the rarity to display size classifications. Where one chooses to place cutoffs for such descriptive classifications is somewhat arbitrary, however for penis size the normal range is medically defined as within 2 SD of the mean, with sizes outside the normal range classified as Abnormally Small or Abnormally Large. Similarly, Micropenis is medically defined as beyond -2.5 SD below the mean, while Macropenis is defined as 2.5 SD above the mean, which each separately correspond to the rarity of ~0.62% of men or an incidence of about 1 in 161 men (technically the definitions of micropenis and macropenis only apply to stretched/erect length, but we may as well apply it to other dimensions too). Additionally, the Theoretically Impossible classification is calculated as the size at which the rarity exceeds that of 1 person in the entire global population of males over 15 years of age (~36.8% of 7.7 billion), which corresponds to roughly 6.2 SD from the mean. This offers a rough estimate of the theoretical limit beyond which sizes are not expected to occur in our global population size, but due to various biological conditions/diseases, such expectations are rarely absolute in biology, and it is likely that these limits are surpassed by individuals in extremely rare cases (much like the largest human height ever recorded was 8' 11", which would be theoretically impossible under the normal approximation to height, since that would be a z-score of well over 12 even when considering just the distribution of heights for men in Western demographics). This person talks more about how the normal approximation may not be perfect for extremes, and hints at a potential issue of our normal distribution's kurtosis and how we might be underestimating the proportions in the extreme tails.
As to the accuracy of the numbers displayed, you should note that while the numbers we display to you are typically rounded, the actual numbers used in these calculations are not rounded and are accurate to the data (you would get a less accurate percentile result if you were to try to calculate it yourself using the rounded average and SD we display).
The Volume
After all that, we estimate statistics for the volume of a penis. The volume of the measurements inserted is calculated using the following formula:
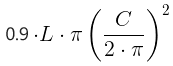
Assuming a perfectly circular girth shape (not the case in real-life), cross-sectional area of the shaft is calculated, then multiplied by the length of the penis to get a cylindrical approximation of the volume. This cylinder is then corrected by multiplying by 0.9 since penises are typically only occupying close to that proportion of a perfect cylinder (obviously this approximation doesn't accurately predict the volume of every penis since some are very non-uniform, however it should on average improve the estimate by correcting for volume reductions from the indentation below the coronal ridge, the conical head, and the imperfectly circular circumference).
The distribution for volume however, is way more complicated. To calculate that, we'd need either paired data of lengths and girths, or a really high level understanding of mathematics to calculate the distribution of the product of two normal variables with a correlation value, which would show how correlated the length and girth measurements are, and we would model a bivariate normal distribution. Unfortunately paired data is not readily available, so this site uses the latter approximation with estimated correlation coefficients to generate the volume distribution. This distribution is very close to normal, however, it has a right skew which can cause large differences in the tails (for constant length and a normal approximation to the volume, to get the same percentile as the bivariate distribution in some cases it can correspond to more than half an inch less girth). This difference is because the distribution of volume is not normal, which is known from the math behind the product of normal variables.
Long story short, the site doesn't use a normal approximation for volume. Instead it has an Excel file of precalculated volumes and percentiles for each dataset.
The correlation coefficients used as estimated from studies are:
BPEL - Erect Girth: r = 0.55
NBPEL - Erect Girth: r = 0.40